https://blog.csdn.net/betarun/article/details/51154003

这方法是昨天听同学提起的，大致翻看了几篇博客跟论文，这里写下自己的理解

从样本相似性到图

根据我们一般的理解，聚类是将相似的样本归为一类，或者说使得同类样本相似度尽量高，异类样本相似性尽量低。无论如何，我们需要一个方式度量样本间的相似性。常用的方式就是引入各种度量，如欧氏距离、余弦相似度、高斯度量等等。

度量的选择提现了你对样本或者业务的理解。比如说如果你要比较两个用户对音乐选择的品味，考虑到有些用户习惯打高分，有些用户习惯打低分，那么选择余弦相似度可能会比欧式距离更合理。

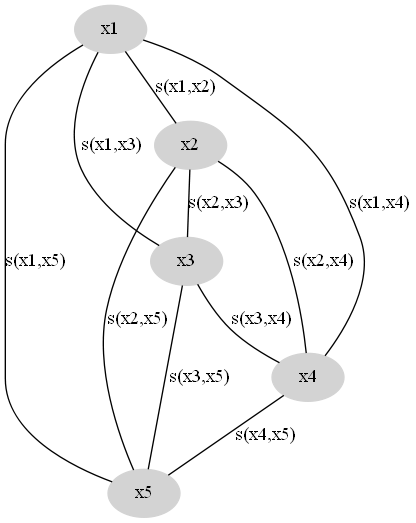
现在我们假设已有的样本为X={

x1,x2,…,xn}X={x1,x2,…,xn}, 我们选择的样本相似性度量函数为(xi,xj)→s(xi,xj)(xi,xj)→s(xi,xj),其中s≥0s≥0,ss越大表示相似性越高。一般我们选择的是距离的倒数。据此我们可以构造相似性图，节点为样本，节点之间的连边权重为样本间的相似性，如图所示。 

这是一个完全图，我们的目的是去掉一些边，使得这个图变成KK个连通子图。同一个子图内的节点归为一类。因此有两方面考虑：

• 子图内的连边权重尽量大，即同类样本间尽量相似
• 去掉的边权重尽量小，即异类样本间尽量不同

一个初步的优化方法是去掉部分权重小的边，常用的有两种方式：

• ϵϵ准则，即去掉权重小于ϵϵ的所有边
• kk邻近准则，即每个节点之保留权最大的几条边

现在我们得到一个较为稀疏的图。 

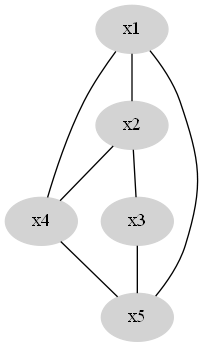
图与图的Laplacian矩阵

为了下一步的算法推导，首先介绍图的Laplacian矩阵，我们记节点i,ji,j连边的权重为wi,jwi,j,如果两个节点之间没有连边，wi,j=0wi,j=0 ，另外wii=0wii=0，那么图对应的Laplacian矩阵为： 

 

L(G,W)=⎛⎝⎜⎜⎜⎜⎜⎜∑nj≠1w1j−w21⋮−wn1−w1,2∑nj≠2w2j⋮−wn2⋯⋯⋱⋯−w1n−w2n⋮∑nj≠nwnj⎞⎠⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜∑nj≠1w1j∑nj≠2w2j⋱∑nj≠nwnj⎞⎠⎟⎟⎟⎟⎟⎟−⎛⎝⎜⎜⎜⎜⎜w11w21⋮wn1